• PR(A) steht für den PageRank einer Seite A,

• PR(Ti) für den PageRank der Seiten Ti, die auf Seite A verlinken,

• C(Ti) für die Gesamtanzahl der Links auf Seite Ti und

• d ist ein Dämpfungsfaktor (Damping Factor), wobei 0 <= d <= 1 ist.

Durch das PageRank-Verfahren werden Websites nicht grundsätzlich in ihrer Gesamtheit bewertet, sondern ausschließlich durch ihre Beziehung zueinander. Der PageRank der verlinkenden Webpages Ti, beeinflusst dabei maßgeblich den PageRank der Seite A.

Die Gewichtung der PageRank-Links Ti, die auf Seite A zeigen, ist dabei allerdings abhängig von der Anzahl C(T) der auf Seite T angeführten Verlinkungen. Je weniger Links eine Webpage T hat, desto mehr gibt sie von ihrem eigenen PageRank an die verlinkte Seite A weiter.

Nun wird der PageRank aller Seiten Ti mit ihrer jeweiligen Wertigkeit addiert. Jeder zusätzliche Link erhöht dabei den PageRank der Page A. Durch Multiplikation der gewichteten PageRanks aller verlinkenden Seiten Ti mit dem Dämpfungsfaktor d, der immer zwischen 0 und 1 liegt, verringert sich das Maß der Weiterleitung des PageRanks von einer Page zur Anderen.

Das Random Surfer Modell

Lawrence Page und Sergey Brin rechtfertigen den PageRank-Algorithmus grob vereinfacht so: Das PageRank-Verfahren ist für die beiden nichts anderes als ein Modell zur Darstellung des User-Verhaltens. Angenommen wird ein User-X, der beliebigen Links folgend, ohne auf Inhalte zu achten, von einer Webseite zur Nächsten gelangt.

Der PageRank beeinflusst dabei die Wahrscheinlichkeit mit der sich User-X auf einer Webpage wieder findet. Die Anzahl der Links bestimmt daher die Wahrscheinlichkeit mit der User-X einem bestimmten Link folgt. Daher fließt der PageRank einer verlinkenden Webpage stets nach der Anzahl Ihrer ausgehenden Links gewichtet in die PageRank Berechnung einer verlinkten Seite ein.

Daraus ergibt sich, dass die Wahrscheinlichkeit mit der User-X auf eine bestimmte Page gelangt, die Summe aller Wahrscheinlichkeiten ist, mit der er von einer linkenden Seite einem bestimmten Link folgt. Durch den Faktor d wird allerdings die Wahrscheinlichkeit mit der User-X auf eine Seite gelangt gedämpft. Die Überlegung dazu ist, dass User-X nicht unendlich vielen Links folgt, sondern zu irgendeinem Zeitpunkt eine x beliebige Webadresse aufruft.

Der Dämpfungsfaktor d, der abhängig von der Höhe der Wahrscheinlichkeit einen Wert zwischen 1 und 0 hat, gibt uns daher an, mit welcher Wahrscheinlichkeit User-X den Links weiter folgt. Je höher die Wahrscheinlichkeit dass User-X Linkss weiter verfolgt, desto größer der Wert d. Da der User-X nach dem Abbruch seiner Linkverfolgung eine beliebige Webseite aufruft, geht die Wahrscheinlichkeit mit der er dies tut, mit dem Wert (1-d) als Konstante in die Kalkulation des PageRanks einer jeden Seite ein.

Abweichende Formulierung des PageRank-Algorithmus

Lawrence Page und Sergey Brin führen in ihren Publikationen allerdings eine weitere Version des PageRank-Algorithmus an. In dieser zweiten Variante errechnet sich der PageRank der Seite A wie folgt:

Dabei steht N für die Zahl aller Seiten des World Wide Web. Diese zweite Variante des PageRank-Algorithmus unterscheidet sich allerdings unwesentlich von der ersten. In der zweiten Variante beschreibt der PageRank einer Webpage im Sinne des „Random Surfer Modells“ einfach nur die effektive Wahrscheinlichkeit, mit der der User-X nach dem Verfolgen unzähliger Verlinkungen eine Seite aufrufen wird. Der zweite Algorithmus zeigt damit die Wahrscheinlichkeitsverteilung über alle Seiten des Internets. Die Summe aller PageRank Werte im Web ist daher bei dieser Variante des Algorithmus gleich 1.

In der erstgenannten Version des Algorithmus, bezieht sich die Bewertung der Wahrscheinlichkeit des Besuchs einer Webpage nach der Anzahl der Seiten im Netz. Der PageRank ist demnach bei dieser Variante nichts anderes als der Erwartungswert für den Besuch von User-X auf einer Webpage, wenn er das genau so oft versucht wie es Seiten im Netz gibt. Angenommen das Internet würde aus 1000 Seiten bestehen, und Page „XYZ“ hätte einen PageRank von 3, so würde User-X bei 1000 Streifzügen durch die Weiten des WWW diese Seite im Mittel drei Mal besuchen.

Die beiden Versionen des Algorithmus unterscheiden sich demnach wie schon gesagt, nicht grundsätzlich. Schließlich gelangt man durch Multiplikation der Zahl aller Webseiten von Variante 2 mit dem PageRank, zum PageRank Ergebnis von Variante 1.

Allerdings ist Page und Brin ist in Ihrer wohl bekanntesten Veröffentlichung "The Anatomy of a Large-Scale Hypertextual Web Search Engine" der Fehler unterlaufen, die erste Version des PageRank Algorithmus als Wahrscheinlichkeitsverteilung zu bezeichnen, bei der die Summe der PageRank Werte aller Seiten im Internet gleich 1 sei.

Im nachfolgenden Beispiel wird die erste Version des Algorithmus angewandt. Da die tatsächliche Anzahl aller Webseiten in diesem Fall keinen Einfluss hat, vereinfacht sich die Berechnung dadurch wesentlich.

Die Eigenschaften des PageRank

Hierfür denken wir uns ein kleines Netz, bestehend aus den Seiten A, B und C, wobei Seite A sowohl auf B als auch auf C verlinkt. Seite B verlinkt nur auf C und C verlinkt auf Seite A. Der Dämpfungsfaktor d wird den Angaben von Page und Brin folgend für Berechnungen üblicherweise auf den Wert 0.85 festgelegt. Um das Beispiel zu vereinfachen, wird d an dieser Stelle ein Wert von 0.5 zugewiesen, wobei der Wert von d zwar direkte Auswirkungen auf den PageRank hat, das hier zu erläuternde Prinzip jedoch nicht beeinflusst. Wir erhalten folgenden Gleichungen für den PageRank der einzelnen Seiten:

Die Lösung des Gleichungssystems ergibt folgende PageRanks für die Seiten:

Wir sehen, dass die Summe des PageRanks aller Seiten, 3 ergibt, und damit gleich der Anzahl der Seiten ist. Dies ist keine spezifisches Ergebnis für unser Versuchsbeispiel, da der PageRank Algorithmus ein Erwartungswert für den Besuch von Seiten bei Anläufen in Höhe der Anzahl der Seiten ist.

Für ein Beispiel mit lediglich drei Seiten, lässt sich ein Gleichungssystem vergleichsweise spielend lösen. Das World Wide Web besteht jedoch bereits aus einigen Milliarden Webseiten, die sich alle paar Monate verdoppeln, was eine Lösung durch ein herkömmliches Gleichungssystem unmöglich macht.

Die iterative Berechnung des PageRanks

Google nähert sich daher der Berechnung des PageRanks auf einer schrittweisen, iterativen Weise. Jeder Webpage bekommt zunächst einen fiktiven PageRank, auf Grund dessen der PageRank aller Seiten im Web im Zuge mehrerer Durchläufe errechnet wird. Diese iterative Berechnung wird im folgenden Beispiel dargestellt, wobei alle Seiten im Netz zunächst den Wert 1 als PageRank zugewiesen bekommen.



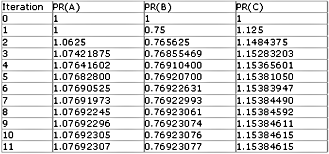
Aus unserem Beispiel ersehen wir, dass die Annäherungswerte bereits nach wenigen Durchläufen sehr nahe an den tatsächlichen Werten liegen. Die Berechnung des PageRanks für alle Seiten des World Wide Web, veranschlagen Lawrence Page und Sergey Brin etwa 100 solcher Iterationen.

Entscheidend ist, dass die Summe der PageRanks aller Seiten nach der Durchführung der iterativen Berechnung gegen die Anzahl aller Seiten konvergiert. Der durchschnittliche PageRank aller Seiten geht daher gegen 1. Jede Webpage hat einen minimalen PageRank von (1-d). Der theoretisch maximale PageRank einer Seite beträgt dN+(1-d), wobei N die Anzahl aller Webseiten ist. Dieser theoretische Wert käme zustande, wenn sämtliche Webseiten ausschließlich auf eine Seite verlinken, und auch diese wiederum ausschließlich auf sich selbst verlinkt.

© copyright 2005 seo-list.de. Reproduktion oder anderweitige Verwendung nur mit audrücklicher schriftlicher Genehmigung.